Energy flow

Energy Flow
What makes concepts such as energy, work, and order so elusive is their insubstantial nature: We find it far easier to visualize the dance of atoms and molecules than the forces and fluxes that determine the direction an extent of natural processes. The branch of physical science that deals with such matters is thermodynamics,an abstract and demanding discipline that most biologists
are content to skim over lightly. Yet bioenergetics is so shot through with concepts and quantitative relationships derived from thermodynamics that it is scarcely possible to discuss the subject without frequent reference to free energy, potential, entropy, and the second law.Thermodynamics evolved during the nineteenth century out of efforts to understand how a steam engine works and why heat is produced when one bores a cannon.The very name “thermodynamics,” and much of the language of this science, recall these historical roots,but it would be more appropriate to speak of energetics,
for the principles involved are universal. Living plants,like all other natural phenomena, are constrained by the laws of thermodynamics. By the same token, thermodynamics
supplies an indispensable framework for the quantitative description of biological vitality.
Energy and Work Let us begin with the meanings of “energy” and“work.” Energy is defined in elementary physics, as in daily life, as the capacity to do work. The meaning of
work is harder to come by and more narrow. Work, in the mechanical sense, is the displacement of any body against an opposing force. The work done is the product of the force and the distance displaced, as expressed
in the following equation:*
W = f Δl (2.1)
Mechanical work appears in chemistry because whenever the final volume of a reaction mixture exceeds the initial volume, work must be done against the pressure of the atmosphere; conversely, the atmosphere performs work when a system contracts. This work is calculated by the expression PΔV (where P stands for pressure and V for volume), a term that appears frequently in thermodynamic formulas. In biology, work is employed in a broader sense to describe displacement against
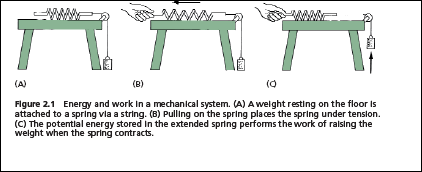
any of the forces that living things encounter or generate mechanical, electric, osmotic, or even chemical potential. Afamiliar mechanical illustration may help clarify the relationship of energy to work.

To understand the energy transformation we need to know the Equilibrium thermodynamics

This will provide information on energy level of a system in initial and final state.

If the final state has a lower energy level than the inItial state, then the process is energetically feasible and can be spontaneous.

That is more energy is given off than it is absorbed

The measure of the energy associated with a particular state is called Enthalpy (H): This can be summarized by the following equation

H = E + PV

Where

E= Internal Energy

P = Pressure

V = Volume ( PV is called pressure volume product

Internal energy (E) include

Velocity or translation kinetic motions of the particles,

electron energies and also absorbed radiant energy.

It is impossible to quantify the absolute internal energy of a substance and therefore it is also impossible to quantify the absolute enthalpy.

The differences in enthalpy between two states (ΔH) can be quantified by measuring the heat released or gained by the systems as it moves between the two states.

Exothermic – Process of releasing heat ,

  Exothermic reaction occurs when they move from a higher enthalpy to a lower enthalpy; they have a negative change in enthalpy (-ΔH).

Endothermic-Processes that gain heat from the surroundings- These reactions occurs when the system moves from a lower to a higher enthalpy, so they have a positive enthalpy change (+ΔH)

Since Enthalpy is a measure of energy , processes that have a (–ΔH) should be  spontaneous because they move from a higher energy state to a lower energy state ( Extra energy is release as heat).

Although some spontaneous have (+ΔH) moving from lower enthalpy to a higher enthalpy , they remove heat from the surroundings. 

The First Law: The Total Energy Is Always Conserved
It is common experience that mechanical devices involve both the performance of work and production or absorption of heat. We are at liberty to vary the amount of work done by the spring, up to a particular maximum, by using different weights, and the amount of heat produced will also vary. But much experimental work has shown that, under ideal circumstances, the sum of the work done and of the heat evolved is constant and depends only on the initial and final extensions of the spring. We can thus envisage a property, the internal energy of the spring, with the characteristic
described by the following equation:
ΔU = ΔQ + ΔW (2.2)
Here Q is the amount of heat absorbed by the system,and W is the amount of work done on the system.Equation 2.2 is a statement of the first law of thermodynamics,which is the principle of energy conservation.If a particular system exchanges no energy with
its surroundings, its energy content remains constant; if energy is exchanged, the change in internal energy will be given by the difference between the energy gained from the surroundings and that lost to the surroundings.The change in internal energy depends only on the initial and final states of the system, not on the pathway or mechanism of energy exchange. Energy and work are interconvertible; even heat is a measure of the kinetic energy of the molecular constituents of the system. To
put it as simply as possible, Equation 2.2 states that no machine, including the chemical machines that we recognize as living, can do work without an energy source.An example of the application of the first law to a biological phenomenon is the energy budget of a leaf.Leaves absorb energy from their surroundings in two ways: as direct incident irradiation from the sun and as infrared irradiation from the surroundings. Some of the energy absorbed by the leaf is radiated back to the surroundings as infrared irradiation and heat, while a fraction of the absorbed energy is stored, as either photosynthetic products or leaf temperature changes. Thus we can write the following equation:
Total energy absorbed by leaf = energy emitted from leaf + energy stored by leaf
Note that although the energy absorbed by the leaf has been transformed, the total energy remains the same, in accordance with the first law.The Change in the Internal Energy of a System
Represents the Maximum Work It Can Do We must qualify the equivalence of energy and work by
invoking “ideal conditions”—that is, by requiring that the process be carried out reversibly. The meaning of “reversible” in thermodynamics is a special one: The term describes conditions under which the opposing forces are so nearly balanced that an infinitesimal change in one or the other would reverse the direction of the process.† Under these circumstances the process yields the maximum possible amount of work.Reversibility in this sense does not often hold in nature,
as in the example of the leaf. Ideal conditions differ so little from a state of equilibrium that any process or reaction would require infinite time and would therefore not
take place at all. Nonetheless, the concept of thermodynamic reversibility is useful: If we measure the change in internal energy that a process entails, we have an upper limit to the work that it can do; for any real process the maximum work will be less.In the study of plant biology we encounter several
sources of energy—notably light and chemical transformations—as well as a variety of work functions, includingmechanical, osmotic, electrical, and chemical work.
In biochemistry, energy and work have traditionally been expressed in calories; 1 calorie is the amount of heat required to raise the temperature of 1 g of water by 1ºC, specifically, from 15.0 to 16.0°C . In principle, one can carry out the same process by doing the work mechanically with a paddle; such experiments led to the establishment of the mechanical equivalent of heat as 4.186 joules per calorie (J cal–1).*
The Direction of Spontaneous Processes
Left to themselves, events in the real world take a predictable course. The apple falls from the branch. Amixture of hydrogen and oxygen gases is converted into water. The fly trapped in a bottle is doomed to perish, the pyramids to crumble into sand; things fall apart. But there is nothing in the principle of energy conservation that forbids the apple to return to its branch with absorption of heat from the surroundings or that prevents water from dissociating into its constituent elements
in a like manner. The search for the reason that neither of these things ever happens led to profound
philosophical insights and generated useful quantitative statements about the energetics of chemical reactions and the amount of work that can be done by them. Since living things are in many respects chemical machines,we must examine these matters in some detail.

Some things happen naturally; some things don’t. A gas expands to fill the available
volume, a hot body cools to the temperature of its surroundings, and a chemical reaction
runs in one direction rather than another. Some aspect of the world determines
the spontaneous direction of change, the direction of change that does not require
work to be done to bring it about. A gas can be confined to a smaller volume, an object
can be cooled by using a refrigerator, and some reactions can be driven in reverse
(as in the electrolysis of water). However, none of these processes is spontaneous;
each one must be brought about by doing work. An important point, though, is that
throughout this text ‘spontaneous’ must be interpreted as a natural tendency that may
or may not be realized in practice. Thermodynamics is silent on the rate at which a
spontaneous change in fact occurs, and some spontaneous processes (such as the conversion
of diamond to graphite) may be so slow that the tendency is never realized
in practice whereas others (such as the expansion of a gas into a vacuum) are almost
instantaneous.
The recognition of two classes of process, spontaneous and non-spontaneous, is
summarized by the Second Law of thermodynamics. This law may be expressed in a
variety of equivalent ways. One statement was formulated by Kelvin:
No process is possible in which the sole result is the absorption of heat from a reservoir
and its complete conversion into work.

The Second Law: The Total Entropy Always Increases
From daily experience with weights falling and warm bodies growing cold, one might expect spontaneous processes to proceed in the direction that lowers the internal energy—that is, the direction in which ΔU is negative. But there are too many exceptions for this to be a general rule. The melting of ice is one exception: An ice cube placed in water at 1°C will melt, yet measurements
show that liquid water (at any temperature above0°C) is in a state of higher energy than ice; evidently, some spontaneous processes are accompanied by an increase in internal energy. Our melting ice cube does not violate the first law, for heat is absorbed as it melts. This suggests that there is a relationship between the capacity for spontaneous heat absorption and the criterion determining the direction of spontaneous processes,and that is the case. The thermodynamic function we
seek is called entropy, the amount of energy in a system not available for doing work, corresponding to thedegree of randomness of a system

References:

1.Lincoln Taiz and Eduardo Zeiger. (2006) Plant Physiology, 4th ed. Sinauer Associates, Inc. Sunderland

2.Horst Marschner (1986) Mineral Nutrition of Higher Plants, 2nd. Ed. Academic Press, San Diego, CA

3.Peter H. Raven, Ray F. Event, Susan E. Eichhorn  (2005) Biology of Plants, 7th.Ed. W.H. Freeman and Co., New York.

4.Salisbury, FB & Ross, CW 1991. Plant physiology 4th Edition Wadsworth Publishing Company.

5.Ross, CW 1974. PlantPhysiology Laboratory Manual. Wadsworth Publishing Company, California.